The new EVLA correlator is extremely powerful in its spectral capabilities. Up to 4 million channels can be observed with a spectral resolution in the Hz regime. Here is a guide to access that spectral line power.

   Contents
   INTRODUCTION
   SYSTEM SPECIFICATIONS
       Receivers and IF System
       The Local Oscillator Chain
       The Correlator
           Total Number of Channels 
       Some Advanced Spectral Line Topics
           Creative Use Of The Spectral Line System
           High Accuracy Spectral Line Polarization Observations
           The Lag Spectrum, Gibbs Phenomenon and Hanning Smoothing 
       Continuum Observations in Line Mode

   OBSERVATIONAL CONSIDERATIONS
       Amplitude and Phase Calibration
       Bandpass Calibration
       Continuum Subtraction
       Interference
       Bandwidth and Time Smearing
       Determining the Observing Frequency
           Doppler tracking and dopset
               Velocity Definition
               Summing Velocities
               Velocity Rest Frame 
           Running dopset
           Setting the LO Chain: loser 
       System Temperature Corrections
           Changes In T$_{sys}$ With Elevation (T$_{spill}$)
           Contributions to T$_{sys}$ From Strong Lines

   REFERENCES
   Bandwidth and Number of Channels
       Normal Mode
       On-line Hanning Smoothing Option

Observation Planning

The wide bands of the EVLA allow users to observe up to 8GHz spectral bandwidth at a time. This will result in extreme continuum sensitivity. In addition, it opens up the possibility to observe one or more spectral lines at a given time. So the first to is to carefully plan the observations.

There are a number of online tools available that help spectral line observers. To start with, the rest frequency of the sopectral line needs to be determined. This can be done with Splatalogue which contains data from the Lovas catalog, the JPL/NASA molecular database], the Cologne Database for Molecular Spectroscopy and others. Note that in addition to molecular line transitions, splatalogue also contains radio recombination lines.

Observing Frequency and Velocity Definitions

The first step is to determine the observing frequency $\nu$ of the spectral line. This is derived from the radial velocity $v$ of the source and the rest frequency $\nu _{0}$ of the spectral line.

A full relativistic calculation shows that the velocity $v$ is determined via $v={\frac {\nu _{0}^{2}-\nu ^{2}}{\nu _{0}^{2}+\nu ^{2}}}$ . This is called the relativistic velocity. This equation is a bit cumbersome to use and in astronomy to different approximations are typically used instead:

Optical Velocity $v^{optical}={\frac {\lambda _{0}-\lambda }{\lambda _{0}}}\,\,c=cz$ ( $z$ is the redshift of the source)

Radio Velocity $v^{radio}={\frac {\nu -\nu _{0}}{\nu _{0}}}\,\,c={\frac {\lambda _{0}-\lambda }{\lambda }}\,\,c\neq v^{optical}$

The radio and optical velocities are not identical. At low velocities that difference is small but $v^{optical}$ and $v^{radio}$ diverge more and more for large values.

At significant redshifts, it is possible to place the zero point of the velocity frame into the source via

$\nu ={\frac {\nu _{0}}{z+1}}$

The redshifted $\nu$ can now be used as the input rest frequency for the observations. The velocites that are derived based on such a redshifted rest frequency will then also be correctly scaled for the spread of the velocity scale that is due to the redshift.

Velocity Frames

The earth rotates, revolves around the sun, rotates around the galaxy, moves within the Local Group, and shows motion against the cosmic microwave background. If one measures a veloocity is is therefore necessary to correct for such motions and define the frame to which the velocities are measured to.

There are various rest frames which might be appropriate. The following table lists their name, the motion for which one has to correct in order to reduce an observed velocity to that particular rest frame, and the magnitude of the velocity correction. Each subsequent rest frame is obtained by adding the effects of the preceding ones:

Rest Frame Name	Rest Frame	Correct for	Max amplitude [km/s]
Topocentric	Telescope	Nothing	0
Geocentric	Earth Center	Earth rotation	0.5
Earth-Moon Barycentric	Earth+Moon center of mass	Motion around Earth+Moon center of mass	0.013
Heliocentric	Center of the Sun	Earth oribtal motion	30
Barycentric	Earth+Sun center of mass	Earth+Sun center of mass	0.012
Local Standard of Rest (LSR)	Center of Mass of local stars	Solar motion relative to nearby stars	20
Galactocentric	Center of Milky Way	Milky Way Rotation	230
Local Group Barycentric	Local Group center of mass	Milky Way Motion	100
Virgocentric	Center of the Local Virgo supercluster	Local Group motion	300
Cosmic Microwave Background	CMB	Local Supercluster Motion	600

The velocity frame should be chosen to what is appropriate for the science. Three frames are commonly used:

Topocentric this is the frame that the sky (observing frequency) uses. It is also the standard for visibilities in the measurement set

Local Standard of Rest is the native output of images in CASA. Note that there are two varieties of LSR: the kinematic LSR (LSRK) and the dynamic (LSRD) definitions for the kinematic and dynamic centers, respectively. The standard used in almost all cases is LSRK and most likely the older LSR naming is identical to the mode modern LSRK definition.

Barycentric is a common frame, too and has virtually replaced the older heliocentric standard. Given the small difference between them, they were frequently used interchangeably.

A full list of reference frames that CASA supports is provided in the CASA reference Manual and Cookbook and also on the casaguides.nrao.edu webpage The most commonly used rest frames are heliocentric (to be precise, barycentric is used at the VLA) and local standard of rest (LSR). LSR is generally used in Galactic astronomy and heliocentric in extragalactic astronomy, although the latter is often reduced to galactocentric.

Doppler Correction

A telescope operates typical at a fixed sky frequency (Topocentric velocity frame). Any spectral line will thus shift during a typical observation campaign. Within a single observation, the rotation of the earth dominates and the line may shift up to ~0.5 km/s (see above). observing campaigns that span longer times, may see spectral lines to shift in frequency by up to 30km/s due to the earth motion around the sun.

Side note: As a rule of thumb, 1 MHz in frequency corresponds to $x$ km/s for the line at a wavelegth of $x$ in mm. E.g. At a wavelength of 7mm, 1 MHz corresponds to about 7 km/s in velocity.

Using this rule of thumb, a line may shift about up to 5MHz in Q-band and up to 0.15MHz in L-band over the course of a year. This needs to be taken into account when setting up the observations. There are different ways to do this:

use the same sky frequency for all observations. The shift of the line is accommodated by a wide bandwidth that covers the line and its width at any time of the observation campaign. The data is later regridded in CASA to a common LSRK or BARY velocity frame. The sky frequency of an observation can be computed with the Dopset tool for a given time. One may find the LST dates on the EVLA Schedule Page.

calculate a different, but fixed sky frequency for each observation. This is called Doppler Setting and offered by OPT (currently only in OSRO mode). The line shift is then minimized to the rotation of the earth (0.5 km/s max). This small shift is corrected again by post processing.

change the sky frequency continuously to keep the line at the same position in the band. This is called Doppler tracking and was standard for the VLA. The EVLA does NOT support Doppler tracking. The WIDAR correlator offers enough bandwidth and spectral channels to cover any line shift and post-processing regridding needs. A non-variable sky frequency delivers also a more robust calibration and system stability.

The post-processing regridding of the line in CASA can be either done directly during imaging in the task clean, or alternatively with the task cvel. This will require that spectral features need to be sampled with at least 4 channels to be correctly reproduced.

Gibbs Phenomenon and Hanning smoothing

For very sharp features, a Fourier transform can prominently display a sinc function, a channel by channel fluctuation of the amplitude. If this is apparent in the data, smoothing adjacent channels will reduce or even eliminate the effect. The smoothing kernel to be used is a Hanning smoothing function which sports a triangular kernel with the central channel being weigthed by 0.5 and the two adjacent channels by 0.25. After Hanning smoothing, however, the channels are not independent anymore and one can eliminate every other channel without losing signal to noise.

In the VLA days, the correlator design could show the Gibbs phenomenon relatively prominently and frequently Hanning smoohting was applied online during the observations to accommodate for the effect and to save disk space. The Gibbs phenomenon is much less common for the EVLA due to a better correlator design of WIDAR. Only very strong maser or rfi sources may exhibit the typical "ringing" feature of the Gibbs phenomenon. In addition, data can be stored rather cheaply so there's no need for data size reduction via Hanning smoothing anymore. As a consequence, the EVLA does not support online Hanning smoothing. If Hanning smoothing is required, it has to be performed in post-processing, e.g. with the CASA task hanningsmooth.

Sensitivity Calculation

The sensitivity of spectral line data is best calculated with the EVLA exposure calculator. This JAVA tool allows you to enter sensitivity limits and provides the required time on source given a frequency, weather, weighting scheme, polarization products, and bandwidth of the observations. The Bandwidth should be the velocity of the resolution that is required to perform the science. This may or may not be the width of individual spectral channels. Overheads need to be added according to our EVLA frequently asked questions webpage. We like to refer to the low frequency guide and high frequency guide for further advise on how to set up the observations, depending on the receiver band to be used.

Correlator Setup

The WIDAR correlator at the EVLA is very flexible and provides a number of setup options that are relevant for spectral line observing.

Basebands

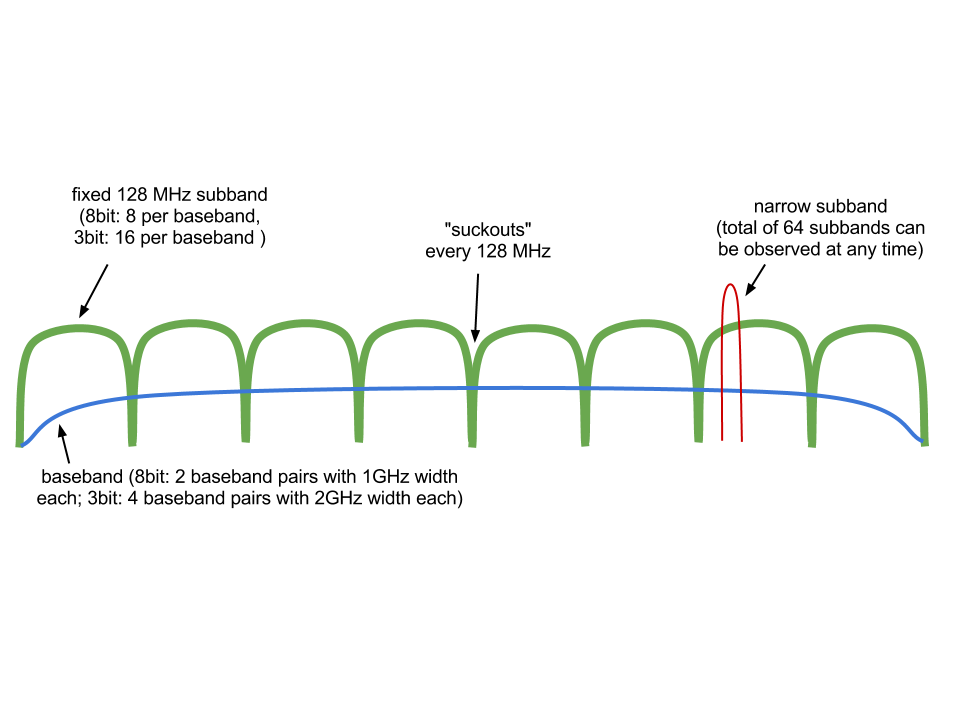
Let's start with the basics: A signal from the telescope enters the WIDAR and during that path, it is passing analog filters that define the basebands. The basebands are actually baseband pairs to cover the L and R polarizations and are the most fundamental spectral ranges for any observations with WIDAR. In the 8-bit mode, WIDAR features two independably tuneable basebands (dubbed AC0 and BD0) with 1 GHz bandwidth each. Using the 3-bit samplers, there are 4 baseband pairs (A1C1, A2C2, B1D1, B2D2), each of them 2GHz wide.

As a second step, the basebands enter digital filters, 128MHz wide, the fixed 128MHz subbands.

Tuning Restrictions

The baseband (pairs) cannot be entirely independently tuned. The following restrictions apply:

3bit samplers can only be used in C-band or above, where the instantaneous frequency width of the receiver is larger than 2GHz.
In Ka band, only one baseband can be below 32GHz and that must be BD
The A1C1 baseband frequency can have a separation of max. 4GHz from the A2D2 baseband. B1D1 and B2D2 have the same restriction of 4GHz separation max.

Fixed 128MHz Subbands and 128 MHz "Suckouts"

After the analog filter that define the basebands, the signal enters the correlator and is split into fixed, 128MHz wide subbands. They are placed adjacently to cover the full width of the basebands. As each fixed 128MHz subband has some filter shape with soft corners, the sensitivity of the EVLA drops to about half its value between any two fixed 128MHz subbands. These frequency ranges are called "128 MHz Suckouts". There are a few options to account and interpolate over the suckouts:

Easiest method is to avoid them in your spectral setup. Try to set the baseband frequency in a way such that any interesting lines do not fall in the suckouts. We have a couple of tools that help, please check the spectral line section of the EVLA RSRO Observing Preparation Guidelines

Observe with two basebands shifted by 10-64MHz apart. This will ensure that at one of the baseband covers the suckouts of the other baseband with full sensitivity. An example is given in the figures. To get more channels, one can consider to use single polarizations on the basebands.

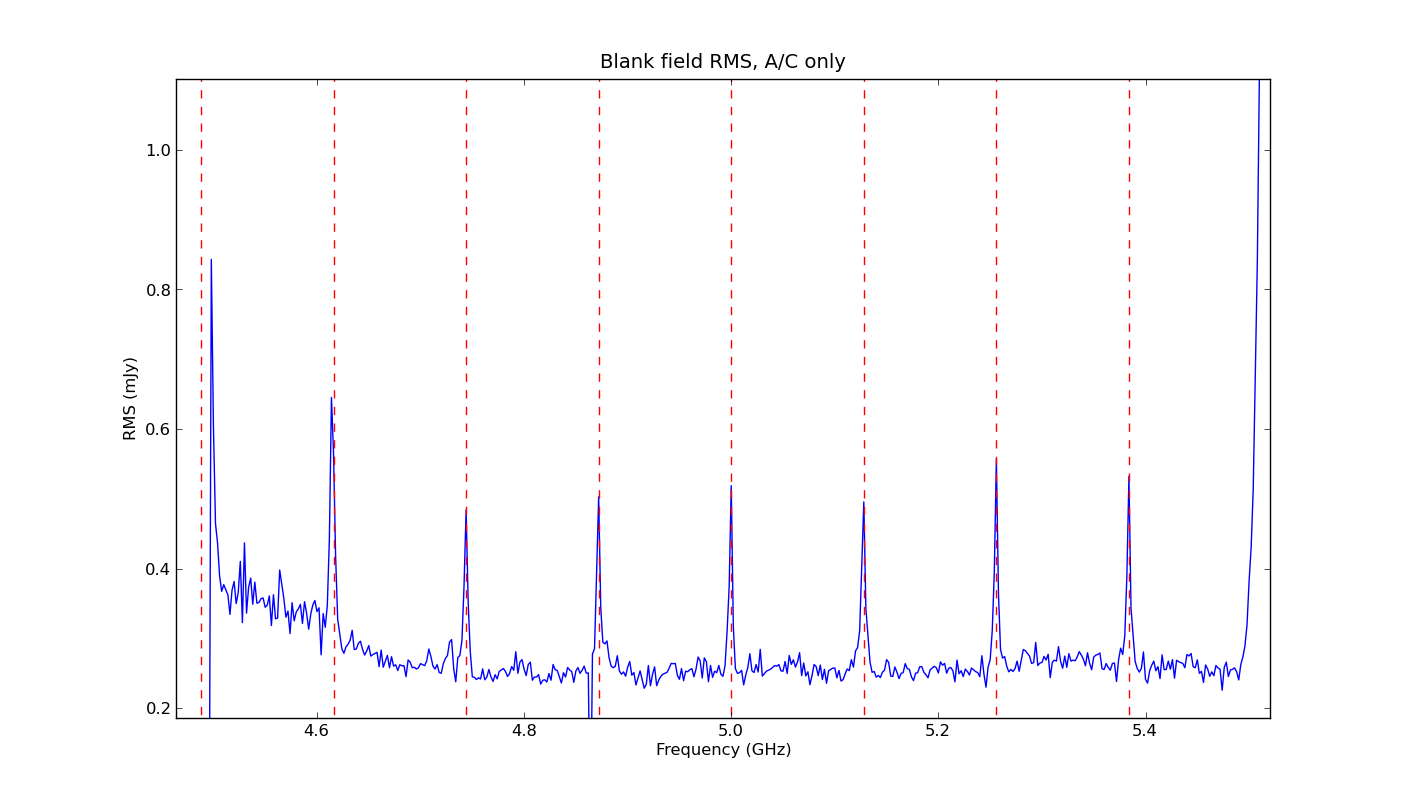
rms noise in a blank field as a function of frequency for one baseband consisting of 8 contiguous sub-bands. Note the increased rms noise at the subband edges.

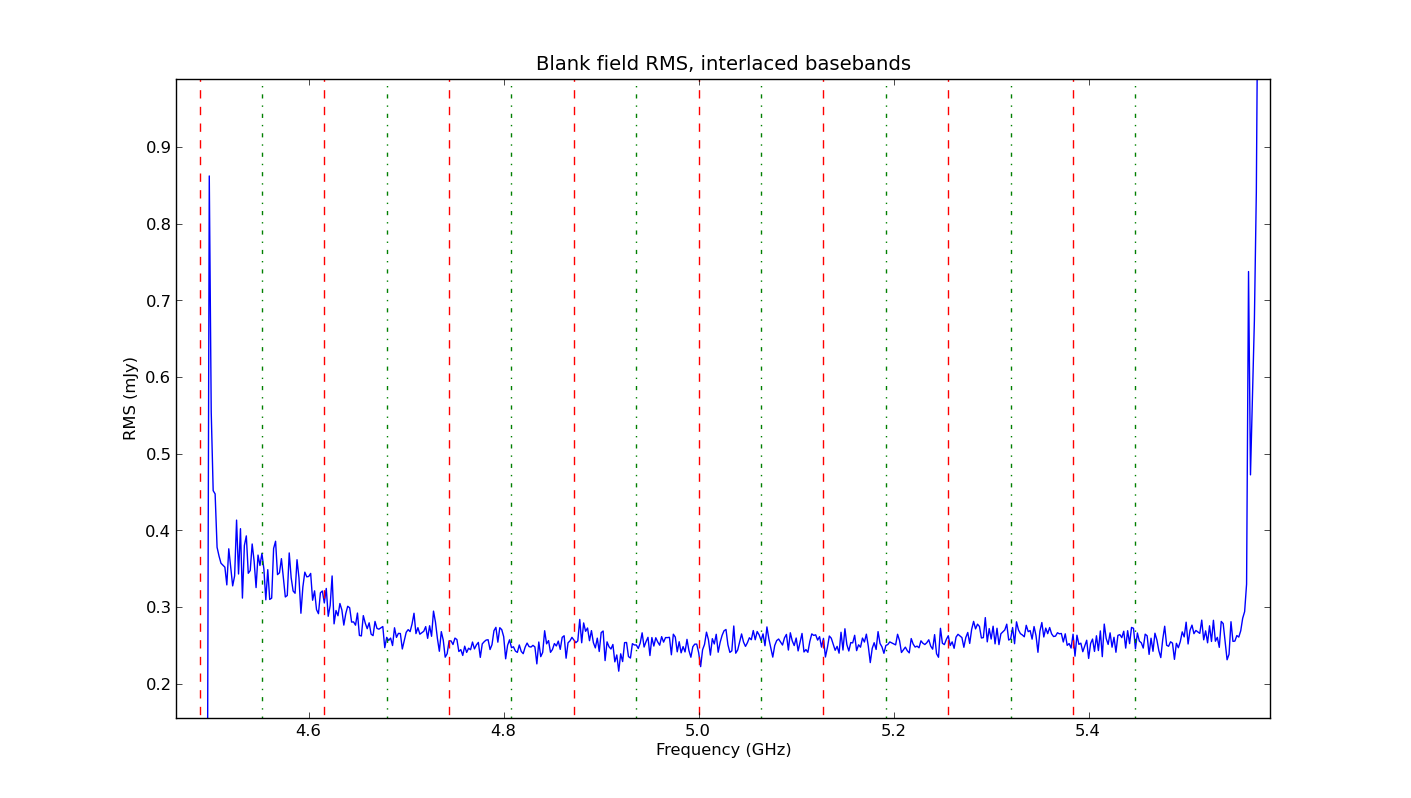
Shifted baseband setup to substitute suckout channels

rms noise in a blank field as a function of frequency for two basebands consisting of 8 contiguous sub-bands, where the basebands are separated by one-half of the subband width. Wherever signal in one baseband is compromised by edge effects, data from the other subband are substituted.

Narrow Subbands

For every baseband, there can be a maximum of 64 subbands. Fundamentally, each narrow subband can be between 128 MHz and 31.25 kHz wide and contains 64 channels when all four RR, LL, RL, LR polarization products are required (full polarization), 128 channel in dual polariation mode (RR & LL), and 216 channelf for single, RR or LL polarization products. The two tables below display the options and the corresponding velocity widths and channelizations:

Full polarization

Sub-band BW (MHz)	Number of channels/poln product	Channel width (kHz)	Channel width (km/s at 1 GHz)	Total velocity coverage per sub-band (km/s at 1 GHz)
128	64	2000	600/ν(GHz)	38,400/ν(GHz)
64	64	1000	300	19,200
32	64	500	150	9,600
16	64	250	75	4,800
8	64	125	37.5	2,400
4	64	62.5	19	1,200
2	64	31.25	9.4	600
1	64	15.625	4.7	300
0.5	64	7.813	2.3	150
0.25	64	3.906	1.2	75
0.125	64	1.953	0.59	37.5
0.0625	64	0.977	0.29	18.75
0.03125	64	0.488	0.15	9.375

Dual Polarization

Sub-band BW (MHz)	Number of channels/poln product	Channel width (kHz)	Channel width (km/s at 1 GHz)	Total velocity coverage (km/s at 1 GHz)
128	128	1000	300/ν(GHz)	38,400/ν(GHz)
64	128	500	150	19,200
32	128	250	75	9,600
16	128	125	37.5	4,800
8	128	62.5	19	2,400
4	128	31.25	9.4	1,200
2	128	15.625	4.7	600
1	128	7.813	2.3	300
0.5	128	3.906	1.2	150
0.25	128	1.953	0.59	75
0.125	128	0.977	0.29	37.5
0.0625	128	0.488	0.15	18.75
0.03125	128	0.244	0.073	9.375

Correlator Baselineboards

Correlator baselineboards (BlBs) are independent units that can be used for separate subbands. WIDAR has 64 BlB pairs (for the polarizations) and thus supports a maximum of 64 subbands.

Baselineboard Stacking

If not all 64 subbands are used, the remaining BlBs can be used to obtain more channels per subband. This method is called "baselineboard stacking" and each additional BlB for a subband adds another 64 channels in full and 128 channels in dual polarization modes. in OPT, this can be set via the BlB.BPS dropdown menu that is available for each subband. Baselineboard stacking is extremely useful as it allows to go to wider bandwidths in each subband but yet maintain a high number of channels. E.g. the full 2GHz bandwidth of the 8bit samplers can be covered by 16 128MHz subbands, each with 128 channels dual polarization as of the table above. The 16 subbands, however, only require 16 BlBs and another 48 are available for baselineboard stacking. One can thus use 4 BlBs for each subbands, quadrupling the number of channels from 128 to 512, or reducing the channel widths from 1MHz to 0.25 MHz over the full 2 GHz frequency range. This method works for any subband bandwidth essentially providng a very high spectral resolution for smaller subbands.

Recirculation

Another way to get more spectral channels for a given subband is called "recirculation". Recirculation uses the fact that the correlator has more computing capability when the data averaged in time. The basic correlator dump time is 1s. If this is doubled to 2s, WIDAR can produce twice as many channels as listed in the tables above. 4s would allow 4 times the number of channels. This setup, however, is not available right now in OPT and EVLA staff needs to be contacted.

Data Rate Limits

The OPT

spectral line setup

- planning - PST - OPT - exposure calculator

- OPT preparation and setup

 . suckouts
 . filters
 . tuneability of subbands
 . channels full/dual/single pol
 . baselineboard stacking
 . recirculation
 . gapfree setups
 . data rate considerations
 . setups with variable bandwidths

- bandpass

- post processing - hanning smoothing - velocity systems - continuum subtraction

Spectral Line Observing

Current->Revised OSS Guidelines

An Overview of the EVLA

(last paragraph) The EVLA correlator will be extremely powerful and flexible. Details of the correlator configurations being offered for EVLA early science during the period Sep 2011 - Dec 012 (a full D→A configuration cycle) are described in Correlator Configurations. It is important to realise that the EVLA correlator is fundamentally a spectral line correlator. The days of separate “continuum” and “spectral line” modes of the VLA correlator are over, and all observations with the EVLA will be “spectral line.” This has implications for how observations are set up, and users who may be used to continuum observing with the VLA are strongly advised to consult Correlator Configurations.

Limitations on Imaging Performance

(Sidelobes from Strong Sources) An extension of the previous section is to very strong sources located anywhere in the sky, such as the Sun (especially when a flare is active), or when observing with a few tens of degrees of the very strong sources Cygnus A and Casseopeia A. Image degradation is especially notable at lower frequencies, shorter configurations, and when using narrow-bandwidth observations (especially in spectral line work) where chromatic aberration cannot be utilized to reduce the disturbances. In general, the only relief is to include the disturbing sources in the imaging, or to observe when these objects are not in the viewable hemisphere.

Correlator Configurations

All observations with the EVLA correlator should be treated as traditional VLA spectral line observations, in that they will require observation of a bandpass calibrator. They may also require observation of a delay calibrator. Users should contact NRAO staff for advice on setting up observations with the EVLA correlator.

Detailed Guidelines

Observing Preparation Recommendations

Scheduling

Calibration Strategy

Bandpass Setup

All observations with the EVLA---even those with the goal of observing continuum---require bandpass calibration. A bandpass calibrator should be bright enough, or observed long enough, so that the bandpass calibration does not significantly contribute to the noise in the image. This implies that, for a bandpass calibrator with flux density S_cal observed for a time t_cal and a science target with flux density S_obj observed for a time t_obj, $S_{cal}{\sqrt {t_{cal}}}$ should be greater than $S_{obj}{\sqrt {t_{obj}}}$ . How many times greater will be determined by one's science goals and the practicalities of the observations, but $S_{cal}{\sqrt {t_{cal}}}$ should be greater by at least a factor of two.

The bandpass calibrator should also be a point source or have a well-known model. At low frequencies, the absolute flux density calibrators (3C48, 3C147, or 3C286) are quite bright and in many cases can double as the bandpass calibrator. However, at high frequencies, these sources have only moderate flux densities of ~0.5--3 Jy, translating into a potentially noisy bandpass solution.

The stability of bandpasses as a function of time is of concern for high-dynamic-range spectral work. We have found that most antennas show bandpasses that are stable to a few (~2--4) parts in a thousand over a period of several (~4--8) hours [L BAND?].

Dramatic jumps in the bandpass structure (of order a few parts in a hundred) can occur at attenuator changes. The observer can track down such attenuator changes in their data using the switched power information; the On - Off power ('PDIF' in AIPS) wil show a clear discontinuity. For this reason, it behooves the spectral line observer to observe a bandpass calibrator at least twice during their observations. Multiple observations will provide a check that all is well on most antennas and a mechanism for identifying any "problem" antennas. However, we do not expect that interpolating in time between consecutive bandpass solutions will bear much fruit for the observer. The low-level variations observed on some antennas tend to not be smooth functions of time and will likely not be corrected with interpolation.

If there is only one observation of the bandpass calibrator, the observer should be careful to minimize the number of shadowed antennas, as an antenna without a bandpass determined for it will essentially be flagged for the rest of the observation.

JuergensSandbox

Contents